In Mathematics, expression is a mathematical statement with at least two terms, including numbers or variables, and are connected by an operator. Addition, subtraction, multiplication, and division are examples of mathematical operators. For instance, x + y is an expression in which x and y are terms separated by an addition operator. Arithmetic expressions, which contain simply numbers, and algebraic expressions, which include both numbers and variables, are the two forms of expressions in maths.
Further, algebraic expressions are divided into monomials, binomials, trinomials, etc. Polynomials is yet another name for them. The distinction between expressions and equations in mathematics is that an expression is made up of a mixture of numbers, such as integers, fractions, exponent, etc. Along with numbers, the expression contains variables and arithmetic operators. In comparison, an equation is made up of two different expressions connected by an equal sign. It implies that the value of the left side expression is the same as the value of the right side. Now, let us discuss how to simplify expressions.
Simplification of Expressions
Simplification of arithmetic and algebraic expressions can be accomplished in two ways. For finding the answer, we can simplify the expression. For example, the expression 6 + 5 – 2 can be reduced to 9. To make them easier to understand, we employ the BODMAS rule.
Similar terms could be added or subtracted in the simplification of algebraic expressions. The like term refers to the same variables raised to the same power. We can easily add or remove two or more like terms by adding their coefficients. For example, 10a + 4a equals 14a. However, 5xy – y is an expression containing two distinct terms that cannot be joined together.
The BODMAS rule is used when several terms and operators are in an expression.
Let’s simplify 42 + 2 – 4 × 5 as an example.
According to the BODMAS rule, first, simply 4 × 5, as there are no brackets or exponents.
Hence, 4 × 5 = 20, and the expression becomes 42 + 2 – 20.
Addition and subtraction are now the only two operators available here.
Since addition and subtraction operations are on the same level, addition is done first from the left side.
Hence, 42 + 2 becomes 44. Our expression is changed to 44 – 20, resulting in 24, which is the reduced answer of the expression 42 + 2 – 4 × 5.
As we all know, a complex number is made of real and imaginary numbers. It’s written as z = a + ib, with a, b as real numbers and “i” as an imaginary number. No real number fulfils the equation i2 = -1 when i = √-1. Various properties of complex numbers, such as reciprocal, equality, and conjugate, help simplify the expression involving complex numbers.
Dividing complex numbers is more complicated than adding, subtracting, or multiplying them because dividing a number by an imaginary number is tricky. When dividing complex numbers, we need to find a term that can be multiplied by the numerator and the denominator to get rid of the imaginary part of the denominator to get a real number in the denominator.
To learn more, subscribe to BYJU’S YouTube channel today!

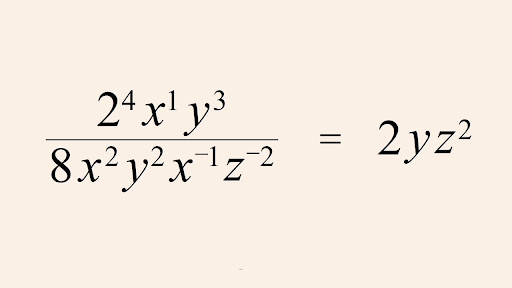
More Stories
Interactive Quran Shikkha for Kids: Bengali Lessons in Quran Memorization and Tajweed
Quran Memorisation Course Online | Learn & Retain with Experts
The Ultimate Guide to AMIRI Hat, Style, Craftsmanship, and Exclusivity